Heap Sort

What is a heap?

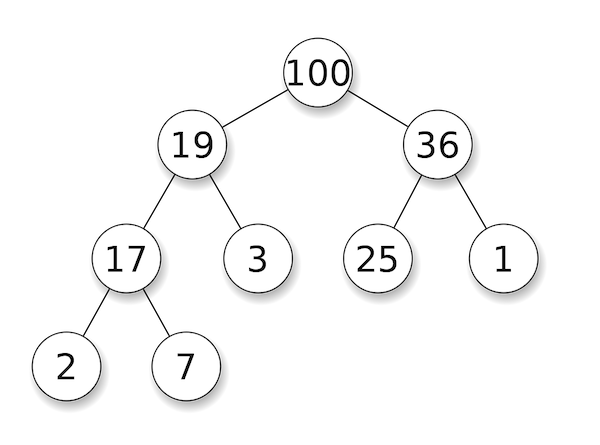
A heap is a tree that has the "heap" property. There can be either max heaps or min heaps. A max heap has the property that for every parent node, it's key is greater than or equal to the key of its child nodes. In other words, in a max heap, the biggest number is at the top.

Max Heap

A min heap is similar to a max heap, except that the parent's key is less than or equal to the child's key. Therefore in a min heap, the smallest number is at the top (or root) of the tree.

What is heapsort?

Heapsort uses a heap data structure in order to perform a sort. It's an in-place comparison sort. The code implementation uses 3 functions: Heapsort, BuildHeap, and Heapify. Heapsort is the main/entry function, BuildHeap forms your initial heap, and Heapify is to make a non-heap tree into a heap. An important thing to recognize is that an array can be a representation of a tree. Imagine arr[0] as the root of the tree and arr[1] and arr[2] as the left and right nodes of the root. Then arr[3] and arr[4] would be the left and right nodes of arr[1], and so on. For example, take the max heap pictured above. In an array representation that would look like:

arr = [100, 19, 36, 17, 3, 25, 1, 2, 7]

Thus, for any given index i, its children are:

• left: 2*i + 1

• right: 2*i + 2

Pseudocode

The pseudocode for the algorithm goes like this: 1. Using the given array, build a heap using recursive insertion 2. Iterate to extract the max element in the heap and then reheapify the heap 3. Extracted elements form a sorted subsequence

Heapsort(Arr)
    BuildHeap(Arr)
    for i in range Arr size down to 1
        swap(Arr[1], Arr[i])
        NewSize = reduce size by one
        Heapify(Arr, NewSize, 1)

BuildHeap(Arr)
    n = Arr size
    for i in floor(n/2) down to 0
        Heapify(Arr, n, i AKA the RootIndex)

Heapify(Arr, i, size)
    max = i
    left = 2i
    right = 2i+1

    if (left <= size) and (Arr[left] > Arr[max])
        max = left

    if (right<=size) and (Arr[right] > Arr[max])
        max = right

    if (max != i)
        swap(Arr[i], Arr[max])
        Heapify(Arr, max)

Code in Python

For working code in Python, visit this repl.

def heap_sort(list):
  # For ease, let's make a variable for the size of the array
  size = len(list)

  # Build inital heap structure
  build_heap(list, size)

  # Loop from length down to 2 to heapify
  for i in range(size - 1, 0, -1):
    #swap first and "last"
    list[0], list[i] = list[i], list[0]

    # Call heapify on reduced list size
    heapify(list, i, 0)

  return list

# Convert array/list to a heap  
def build_heap(list, size):
  for i in range(size // 2, -1, -1):
    heapify(list, size, i)

# Make our tree into a max heap
def heapify(sublist, size, root_index):
  largest = root_index
  left = 2*root_index + 1
  right = 2*root_index + 2

  if(left < size and sublist[left] > sublist[largest]):
    largest = left
  if(right < size and sublist[right] > sublist[largest]):
    largest = right

  if(root_index != largest):
    sublist[largest], sublist[root_index] = sublist[root_index], sublist[largest]
    heapify(sublist, size, largest)


# Test Data
print(heap_sort([8, 2, 1, 4, 6, 5, 7, 3, 22, 1, 19, 3, 33, 7, -3, 111, 21, -4, 0, 99, 89]))

References

• Pseudocode Source

• Coding Geek Implementation/Explanation

• Example Code